津田一郎の『千夜千冊エディション』を謎る⑥ 『編集力』でアブダクションを謎る

2025/10/15（水）08:00

1. 推論＝心？
   

   『編集力』には編集工学の技法がいっぱい詰まっている。この450ページを超えるエディションを読み込めば、松岡さんの思想と技法が会得できるのではないか。だとすると、これは恐ろしいエディションである。謎ることすら気が引けるが、そもそも「エディションを謎る」の趣旨からいえば気が引けていては意味がない。ここはもう思い切るしかない。数学ではこれを割り切るという。漱石は10割る3を引き合いに出して、世の中の割り切れなさを表現したが、今回は10÷３＝３とでもして割り切ることにする。

   
   

   アブダクションはチャールズ・パース（1839年―1914年）の発案による推論形式の一つだ。松岡さんはパース自身の著作に触れ、パースの関心は一から十まで推論の正体を見極めることだと書いている（第1182夜、『編集力』pp267-294）。そして、パースは自意識や心までも複雑な推論プロセスと捉えられるとみなした最初の哲学者だと書いた。また、パースが最も重視した推論がアブダクションとレトロダクションだと言い、これに「推感編集」という言葉を当てた（第508夜、『編集力』pp257-266）。まさに、「問う」ということ自体が推論であり、編集の根本的な構造であると主張した。この考えは安藤昭子『問いの編集力』（ディスカヴァー・トゥエンティワン、2025年）に引き継がれた。そうならば、推論＝心と割り切ってもよいだろうか。『シャーロックホームズの記号論』（第508夜、『編集力』pp257-266）は私にとっても懐かしい書物である。私は松岡さんと初めて会った時、カオス力学を基軸にして脳研究を行おうと決めていたが、従来の科学とは異なる方法論が必要だと感じていて、2年後の1984年に”A hermeneutic process of the brain”という論文を世に問うた。まさにこの解釈学的観点からシャーロックホームズのような探偵が行う推論の仕方を脳で起こっているダイナミックな情報の問題として定式化したいと思ったのだった。しかし、よくよく考えてみると、探偵がやっている推論、すなわちアブダクションは自然科学者が自然現象を理解するときの推論、数学者が定理を証明するときの推論ときわめて類似し相似関係にある。松岡さん言うところの、ルイジ君とソージ君だ（例えば、第1642夜、『編集力』pp.209-223）。ただ、可能な多数の仮説の中からどの仮説を選ぶかという基準が、自然科学においては実験事実を最も簡潔に説明する理論であり、数学においては美しい証明によって演繹が完成するような命題である。「最も簡潔に」とか「美しい証明に導く」とかあいまいな表現であるが、自然科学や数学においては仮説の選択はこうやって行われてきたのである。解釈学的に言えば、「もっともらしさ」であろうか。

   
   

   私としては、推論＝心を最初に追求したのはブール代数で有名なジョージ・ブール（1815年―1864年）であろうということを指摘しておきたい。少なくともパース以前で明確にその意識があった人として。むろん、デカルトやアリストテレスも近い感覚をもっていただろうが、心や意識を推論と等置した最初の人はブールだったのではないだろうか。その後、パースが出現する。ブールはその著書、“An Investigation into the Laws of Thought, on which are founded the Mathematical Theories of Logic and Probabilities”（Walton & Maberly, 1854年）において、本来なら無限の概念を基盤にして構築すべき確率論を０と1の二値のみから再構成しようと試みた。出発点は“白い白い”＝“白い”であるかと問うことだった。これは“白い”を二回心の中で反復した時、心に浮かぶ白さは“白い”と一度心の中で言った時の白さと同じかどうかという問いである。“白い”を記号Xと置くと、XX=Xかと問うことになる。ここで、ブールはXに対して”白さの確からしさ”のようなものを想定していたようだ。XXという記号Xの並置に掛け算という代数演算の意味を持たせたのだ。突如、異なる空間への飛躍である。意味を確定させるための集合論に取り換えたと言ってもよい。代数となれば計算ができ定量化ができる。X×X=X、つまり、X²=Xの解はX=0と1である。ちゃんと二値が出てきたではないか。これをもとの集合で意味付けすると、“白い白い”に対する”白さの確からしさ“は”白い“に対する白さの確からしさと”全く同じ“（X=1に対応）か”全く異なる“（X=0に対応）かのいずれかだということになる。二度叫んで同じ心情になるか、いや全く違う心情になるか、だと。中間はない、と主張したのである（拙著『心はすべて数学である』（文春学芸ライブラリー、2023年））。ここを出発点にして、連続値を扱う確率論を構成できるならば、中間の心情に対してもこの二値に基づく推論を”うまく“繰り返して書き尽くすことができるだろう。こうやってブールは推論＝心を達成しようとしたのである。

   
   

   このブールの著作は表題にあるように、まさに「思考の法則」を明らかにしようとしたもので、しかもブールにとっては思考＝推論＝心であったのである。この考え方は現在のデジタルコンピューターの数学的基礎を作ったアラン・チューリング（1912年―1954年）に引き継がれていった。パースがブールの研究をどこまで知っていたかは分からない。しかし、次のような事情を考えるとつながりがあったのではないかと想像したくなるのである。ブールの前掲書が出版されたときパースは15歳であった。アブダクションについては、それまで知られていた演繹と帰納とは異なる推論方法だが、数学や自然科学、社会科学、人間科学に不可欠な新たな推論方法だという認識を1866年（ブールの死後二年目）には確立していたという（シービオック・シービオック著『シャーロックホームズの記号論』、岩波現代選書、1981年）。しかも、ブールは当時科学の先進国であったイギリスで活躍した数学者であり、パースは科学の発展途上国であったアメリカの哲学者、論理学者、数学者、実験心理学者、工学者、経済学者でもあったことを併せ考えると、影響がなかったと考える方が不自然である。

   
   

   ブールと言えば昨年（2024年）ノーベル物理学賞を受賞した人工知能学者のジェフリー・ヒントンを連想する。彼の父方の曾祖父の妻の父親がジョージ・ブールなのである。なんというつながりであろうか。現代の連想記憶・推論をニューラルネットによって可能にした生成系AIの基盤を作った一人が思考の法則のジョージ・ブールの遠縁であったのだ。さらに、面白いのは、ジョージ・ブールの妻メアリ・エベレストは思考＝推論＝心なる等式をも打ち砕くチョモランマが世界最高峰の山であることを測量によって発見したジョージ・エベレスト（1790年―1866年）の姪なのである。

2.  

   

   チャールズ・サンダース・パース(左図)。ボストンからニューヨークに向かう船でコートと時計を盗まれたため、あらゆる手段を講じて犯人を追い詰めていく（推論する）リアル・ホームズを演じたこともある。
   ジョージ・ブール[George Boole](右図)。ブールはキリスト教の一種であるユニテリアンの家系に生まれた。ユニテリアンは三位一体論を否定し、神はただ一つ（＝ユニ）であると考える。ブールは代表作『思考の法則』で、あらゆる存在を神かそれ以外かで二分する世界観を論理の基礎としたことで、人間の思考を代数で表現する可能性を切り拓いた。
3. 
   

   推論とは何だろうか？

   松岡さんがパースの志向性に注目したのは、パースが思考のすべては推論のプロセスだ、意識も推論なのだ、と言っている点だ（第1182夜、『編集力』pp.267-294）。そして、その推論のプロセスに三つの推論形式、演繹推論、帰納推論、仮説推論を考え、それら全てが機能するように編集されたものが推論だとしているところなのだ。それで、松岡さんはわざわざ、このパースの志向性を「推感編集」と名付け、「パースの推論では、感覚や知覚が注意によって編成され、さらには再編成されていく。注意のカーソルがたどるダイナミックな編集プロセスを観察するという作業が推論において起こっている」と読み解いた（第1182夜、『編集力』pp.267-294）

4. この指摘は、Transformerに代表される現代の生成系AIと共通する部分がある点で非常に示唆的である。松岡さんとの共著『初めて語られた科学と生命と言語の秘密』（文春新書、2023年）のもとになった対談では、なぜか生成系AIに互いに踏み込むことをしなかった。今ならパース、ブール、チューリングを引き合いに出して、今後のAIを見据える議論ができたのではないかと思う。いや、あの時点でもやっておくべきだったのではないかと、ちょっと悔やまれるところではある。

   
   

   演繹は英語でdeductionという。”duction”は”to lead”、導くことだ。”de”は”from”の意なのでdeductionは“そこから導くこと”、つまり、前提があって、そこから導くことで何らかの結論を得ることである。帰納はinductionだが、”in”は”to”とか”toward”の意なので、inductionは“そこへ向かって導くこと”、つまり演繹推論とは逆に、結論を前提としてそれを成立させているもとの前提を一般化することで探ることである。仮説推論はabductionだが、”ab”は”away”の意なので、abductionは“持ち去ること、連れ去ること”。それで、abductionには誘拐の意味もあり、この言葉の使用を敬遠する向きもある。それだからか、パース自身も後にretroductionと言い換えたりしている。これは遡及的に推論することを意味し、「Aが起こったからBが起こった」という因果的事象に対して、「Bが起こったならその前に何が起こったのだろうか、Aなのか？」と時間をさかのぼって推論することである。一見、帰納推論と似て見えるので多くの人が誤解している。実はパース自身も帰納推論と仮説推論を混同していたと告白している（シービオック・シービオック著『シャーロックホームズの記号論』、P.35）。研究者でもしばしば誤解していると思われる記述がある。むろん、松岡さんは誤解していない。

   
   

   さて、このような日常的な出来事に対する推論と古典論理としての仮説推論（アブダクション）とが同じものであるとすると大いに違和感を覚えるだろう。違和感の原因は古典論理の形式性と日常の推論の因果性にある。古典論理のアブダクション、仮説推論は演繹推論同様トートロジーであるので常に真であるが、日常の仮説的な推論では必ずしも真に至らない。また、古典論理の推論規則「AならばB」には因果関係はなく、論理が働く集合間の包含関係にすぎないが、日常の推論における「ならば」は因果関係を意味している。

   
   

   パース自身の説明を聞こう

   では、パース自身はどう説明していただろうか。1867年に発表された論文、”On the Natural Classification of Arguments”（Proceedings of the American Academy of Arts and Sciences v. 7, (1867)pp. 261–287）において、パースは次のように三つの推論を記述した。例として、その後定着した主語－中項―述語関係を挙げた。三段論法は前提と結論を推論規則で結ぶ推論形式だが、前提は大前提と小前提からなる。大前提は一般的な命題、小前提は具体的な命題である。二種類の前提に現れるが結論には表れない概念を中項（M）と呼ぶ。例えば、主語（S）として「ソクラテス」をとり、述語（P）として「死ぬ」をとると、大前提：「すべての人（M）は死ぬ（P）」、小前提：「ソクラテス（S）は人（M）である」から結論：「ソクラテス（S）は死ぬ（P）」が導かれる。これが演繹推論だ。この場合は「人（M）」が中項（middle）である。これに対して帰納推論は次のようになる。中項である「人」として、無作為に何人かを選ぶ。たとえば、「人」（M）であるソクラテス１（S1），ソクラテス２（S2），ソクラテス３（S3）を選ぶ。これら三人が死んだとしたとき、「すべての人（M）は死ぬ（P）」と一般化するのが帰納推論である。この例はあまりにも当たり前に見えるが、例えば、ソクラテス1（S1）は50歳で死んだ（P1）、ソクラテス2（S2）は75歳で死んだ（P2）、ソクラテス3（S3）は80歳で死んだ（P3）、という事実から、「すべての人（M）は100歳までには死ぬだろう（P）」という一般化もある。これは必ずしも真とはならない。

   
   

   アブダクションのことをパースはこの論文ではhypothesis（仮説）と呼んでいるが、ここではアブダクションとする。さて、アブダクションは次のような推論だとした。「すべての人（M）は例えば、やがて死ぬ（P1）、二足歩行動物である（P2）、さまざまな記号によってコミュニケーションを行う（P3）、食物をとる（P4）」であり、「ソクラテス（S）はやがて死ぬ（P1）、二足歩行動物である（P2）、さまざまな記号によってコミュニケーションを行う（P3）、食物をとる（P4）」から「ソクラテス（S）は人（M）である」と仮説することである。帰納推論が、結論と小前提から大前提を導こうとする（一般化する）のに対して、アブダクションは、結論と大前提から小前提を導こうとする。大前提は誰もが納得する一般論であるなら、それに疑いをはさむことは合理性を欠くので得られた結論と共に前提に入れてよいだろう。こうやってより具体的な小前提を推論するので、あてずっぽうとは違うのである。むしろ仮説推論は論理的には真であると同時に、現実の推論としても合理的な推論方式である。それに対して、帰納推論はより一般的な大前提を具体的な小前提と結論から導こうとするので、あてずっぽうの要素が入り込む余地がある。帰納推論は、論理としても現実の推論としても必ずしも真なる命題を導くとは限らないのである。

   
   

   1878年の論文ではもう少しすっきりした記述になっている。”Deduction, Induction, and Hypothesis”（Popular Science Monthly, v. 13, （1878）pp. 470–82）

5.  

   演繹推論

   前提（パースはruleという言葉を使っているがこれは推論規則の事ではない。これが多くの誤解を与えている理由の一つかもしれない）：「この袋の豆はすべて白い」

   条件分岐（caseという言葉は条件が真であるときに行う操作であるので、むしろ推論規則に対応する）：「これらの豆はこの袋から取り出された」

   これから次の結論が導かれる。

   結論（result）：「これらの豆は白い」

   
   

   帰納推論

   条件分岐：「これらの豆はこの袋から（ランダムに）取り出された」

   結論：「これらの豆は白い」

   これから次の前提が想像される。

   前提：「この袋の豆はすべて白い」

   むろん、この推論は必ずしも正しくないことは明白であろう。

6.  

   仮説推論（アブダクション）

   前提：「この袋の豆はすべて白い」

   結論：「これらの豆は白い」

   これから次の条件分岐（推論規則）が得られる。

   条件分岐：「これらの豆はこの袋から取り出された」

   これはまさに合理的判断であり、仮説生成にあたるのである。

7.  
8. 

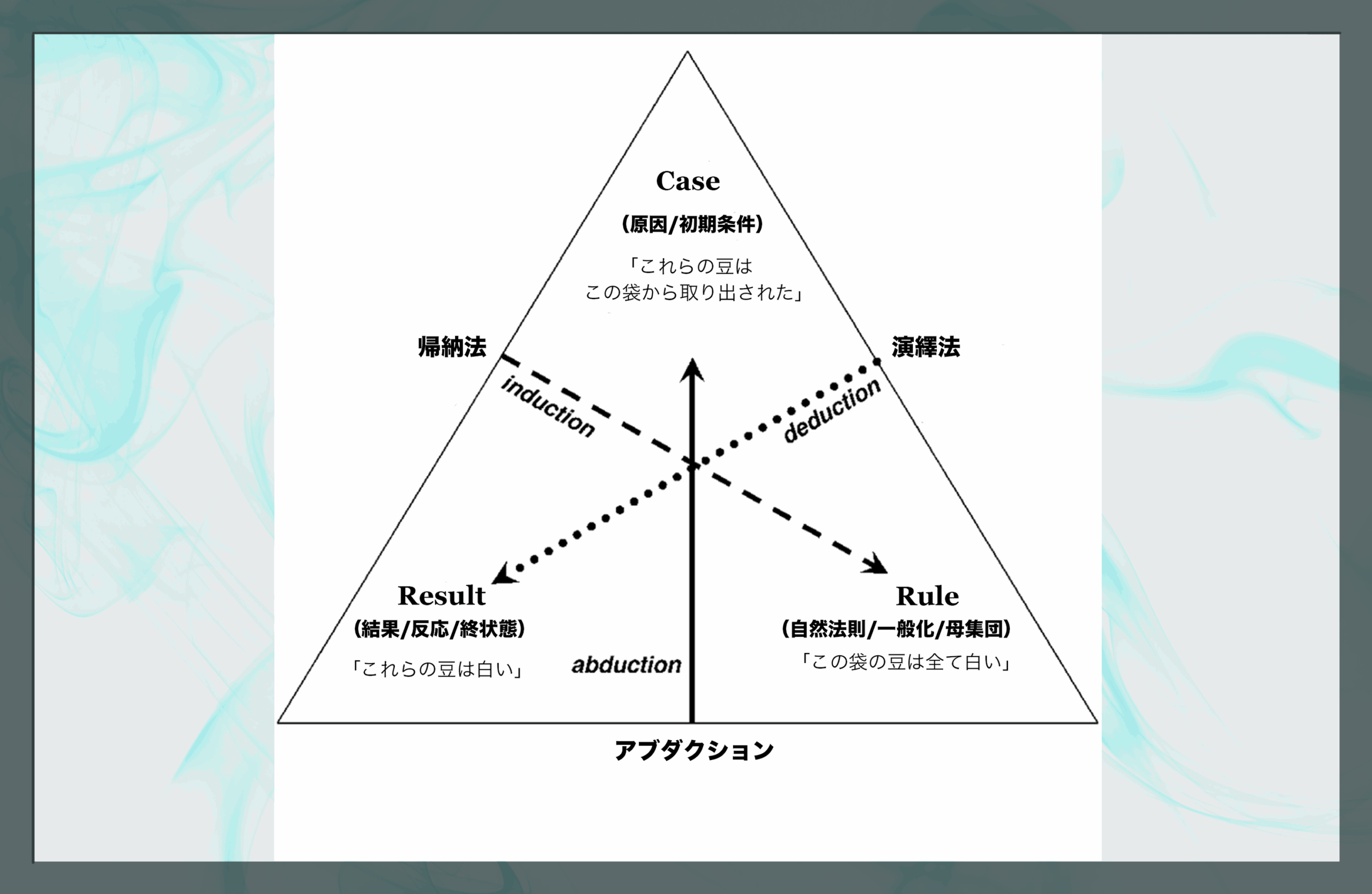
   演繹、帰納、アブダクションの関係図。この三角形の頂点(Case, Result, Rule)のどれか二つが与えられ、残り一つが不明であるとき、その一つを明らかにするのが推論である。たとえばアブダクションを表すのは底辺から垂直に伸びる実線の矢印である。三角形の左下(Result=この豆は白い)と右下(Rule=この袋の豆は全て白い)が与えられているので、アブダクションは不明である頂点(Case)を「この豆はこの袋から取り出されたのでは？」として導くのである。演繹の点線矢印とアブダクションの実線矢印は右下のRuleを共有している。これは法則であり常に正しいものとして取り扱う（袋の中にたまに黒い豆が混ざっていることはありえないものとする）ので、論理学上は演繹もアブダクションもトートロジー、つまり論理的な正しさは絶対に保証されるのである。日常的に使われる「仮説」という言葉には、さまざまな具体的事象から背景にある法則性を見破るニュアンスが強く、むしろ論理学上は帰納に近い。
   （Kleinhans et al., 2010, Hydrology and Earth System Sciences, Fig. A1 を改変して作成, CC BY 4.0）

9.  

   三段論法再び

   前回（第5回）の最後に、三段論法を基盤にして、演繹推論、帰納推論、仮説推論の真理値を説明した。三段論法は今回説明しているように、大前提「MはPである」、小前提「SはMである」、よって結論「SはPである」というように、中項Mを消去する推論規則で特徴づけられる。まず、この形式は前回の形式と同じであることを確認しておこう。前回の三段論法の形式は「AでありかつAならばB、であるならばBである」というものであった。この形式では、Aが大前提に対応している。「AならばB」は小前提であり、Bが結論である。この形式では、A, Bには中項があるようには見えないが、それらを具体的な命題として書き下せば中項の存在が見えてくる。例えば、A:「すべての人は死ぬ」、AならばB：「すべての人が死ぬならば人であるソクラテスは死ぬ」。この両者が正しいとするとB:「ソクラテスは死ぬ」となるのである。「AならばB」が成立するということは人の中からソクラテスを選んだということである。そこで、「AならばB」は中項から具体例を選ぶ行為を意味すると捉えるとよいだろう。

   
   

   数学、自然科学における推論とアブダクション

   パースは仮説推論、すなわちアブダクションは数学や自然科学における仮説形成の基盤であると考えていたようだ。私も「脳の解釈学」（I. Tsuda, Prog. Theor. Phys. 1984）の論文を発表する時点で、似たようなことを考えていたことは本エッセイの最初で述べた。ここをもう少し整理しよう。自然科学では、実験によって（その実験が成立するという条件付きではあるが）いくつかの事実が得られる。これらからこの事実の背後にある自然法則を推定する時、帰納推論とともにアブダクションを使用する。得られた実験事実を導く一般規則（小前提）を想定したうえで、それを成り立たせるべき理論（大前提）を想定する。これは帰納推論だが、必ずしも正しくないことがある。そこで、すでに確定している理論、あるいは蓋然性が高い（もっともらしいと思われる）理論（大前提）の仮定のもとで、実験事実を導く一般則（小前提）を仮説として推測する。これがアブダクションである。仮説した一般則はさらに実験で検証できる。大枠である理論そのものの検証は非常に難しく、上の過程を何度も繰り返すことで理論の蓋然性（もっともらしさ）をさらに高めていくしかないのである。この理論そのものを想定することが帰納推論にあたるのだ。世間でよくみられる誤解は、これをアブダクションだと想定していることである。

   
   

   では数学はどうか。コンピューターを使って数学的事実を集めることで定理を推理する応用数学では自然科学と同じ方法が機能する。他方、純粋数学では帰納推論はカンを働かせるためにのみ使われる。論理的には正しくないから方法論としては使えない。学校教育の証明問題では、仮定（大前提）と結論が与えられて、それをつなぐ論理（小前提）を考える。このアブダクションの段階ではこの小前提が仮説に対応し、小前提の正しさをlemma（レンマ、補題）として確定するために演繹推論が使われる。実際、数学者が研究で行っている推論も似たところがあるのである。仮説はいくつもあり得る。つまり、想定した大前提（公理や他の定理）と定理として証明したい命題（結論）を仮定してみて、それをつなぐ論理の鎖（小前提）を考えるのだから、複数の論理の鎖があり得るのである。証明の仕方は複数あるということだ。選択の基準は美的センス意外にはありえない。古典論理においてアブダクションはトートロジーであるので、同じトートロジーである演繹によって正しさが確定するのである。では編集工学ではどうか。編集工学は数学ではないし、自然科学のような実験科学でもない。しかし、編集の過程で物語を構成してみるなど実験的要素はある。また、数学的な論理の一貫性も時に必要になるだろう。そうしておかないとここぞというとき（今まで見えなかった物語が突然見えてきたり、従来とは異なる関係性が見えたり）、論理からの飛躍はできないからだ。編集工学においてもアブダクションは多くの仮説を生成するが、選択の基準は、豊富な物語性＝より深い問い、にこそあるだろう。

『不思議の国のアリス』の著者ルイス・キャロルは、三段論法を図で解くキャロル・ダイヤグラムを考案した論理学者でもあった。おかげでアリスは「論理の誤謬」に満ちた物語となっている。帽子屋のなぞなぞ「カラスと書き物机はなにが似ている？」は、Result（カラス≒机）だけを提示し、Case（理由）を考えさせる問題であり、鍵となるRule（＝似ている）を未定義のままにしている。作中では解けないままだが、後年多くの読者が掛け言葉説や倒語説、E.A.ポー説など多様な文脈からアクロバットな回答を編み出してきた。科学においてはアブダクションで仮説を生み出したら、検証と整合性によって仮説を絞り込んでいく。一方、編集におけるアブダクションは断片（Result）と文脈（Rule）のあいだに仮説（Case）を無数に張りめぐらせ、問いをさらに開いていく。アリスに仕込まれた数々のお題は、読者に〈問いの連鎖〉を起こす編集的アブダクションの原型なのである。

1.  

2. 図版構成：梅澤光由

    

§津田一郎の新刊情報

『脳から心が生まれる秘密』（幻冬社新書）2025年9月25日刊行

YouTube（ReHacQ）にて「脳から心が生まれる秘密やカオス理論、脳の進化に必要な不自由など」について語っています。 

【AIvs人間】AIは心を持つのか？脳と心の仕組みを解き明かすカオス理論を使った最新研究

1.  

   津田一郎の『千夜千冊エディション』を謎る

   ①『心とトラウマ』に西洋と東洋のAIDAを謎る

   ②『心とトラウマ』に「心の統合」という不思議を謎る

   ③『理科の教室』で偶然の一致あるいは縁を謎る

   ④『理科の教室』で遍歴を謎る

   ⑤『理科の教室』で思索の庭を謎る

2. ⑥『編集力』でアブダクションを謎る