津田一郎の『千夜千冊エディション』を謎る⑨ 『編集力』で負を謎る

2026/01/15（木）21:32

アフォーダンスと環世界
アフォーダンスは編集工学の３Aの一つだ。環境が生物に与える行動的意味や価値のことだ。アフォーダンスは知覚者の状態には依存しない。ギブソンの本来の考えとして、アフォーダンスは生物と環境の間にある行為に関する関係性を表しているが、アフォードしているのはあくまで環境の方である。ギブソンは「生態学的心理学」を構築する過程でアフォーダンスの研究を重視した。それは、物が物に囲まれるのと違って、生物が物に囲まれると主体である生物が物から受ける情報を物との関係性でしか捉えられなくなるという“「包むもの」や「囲むもの」をめぐる包摂”という考え方に至ると松岡さんは読み解いた（第１０７９夜、『編集力』pp.176-185）。するとユクスキュルの環世界（第７３５夜、『デザイン知』pp.80-88）との関係が気になってくる。AIDAシーズン６の第二講の講評で安藤昭子氏がアフォーダンスと環世界が関係すると短く触れたことは偶然ではない。この二者は大いに関係する概念である。

環世界は環境世界のことで、個々の動物種によって環境世界から得られる情報は個々の種において独特に発達した感覚知覚器官に依存している。それ故に動物を取り巻く環境と言っても全く異なる世界と考えるべきである。個々の生物種ごとに、いや個々の生物ごとに環世界がある。おそらくこれは植物にも当てはまるすべての生物の情報獲得・行動原理の基礎になる概念である。

アフォーダンスは環境が生物に促す行為であるならば、ベクトルの向きは環境から生物にある。環境をA、生物をBとベクトル表記したとしよう。するとアフォーダンスはarg⁡(B-A)なる方向を持つ。ここでarg(X)はベクトルXの角度を表している。これに対して、環世界のベクトルの向きは生物から環境へ向かっているので、arg⁡(A-B)である。アフォーダンスのベクトルを180度（πラジアン）回転させたものである。すなわち、arg(A-B) =arg(B-A)+πである。中島秀之はアフォーダンスと環世界はベクトルの向きが逆だと言った。上の式はこのことを端的に表したものだ。アフォーダンスにおいては環境に対して生物は点である。他方、環世界では生物に対して環境は点である。こう考えると、アフォーダンスと環世界はある種双対関係にあるように見える。

ところがである。ユクスキュルは生物（種）個々の知覚活動は環境によって作られた「抜き型」であって、「負の型」と呼ぶにふさわしいものだと考えたというのだ（第７３５夜、『デザイン知』pp.80-88）。この「負の型」でしか個々の生物は世界を見ることはできないので、環境との相互作用もそこに限定される。そうすると、環境が与えた「負の型」が生物に対する環境からのアフォーダンスだと考えてよいのではないか。つまり、arg⁡(A-B)は「負の型」を表しているのだから、「正の型」でみればもう一度180度回転させて、 arg (A-B) +π=arg (B-A) +2π=arg⁡(B-A)、すなわちアフォーダンスである。むろん、(B-A)=-1×(A-B)と考えてもよい。この時は、「負の型」を「正の型」でみるために-1を掛けるという変換を行ったと考えるのだ。-1=e^iπ, i=√-1（虚数単位）だから、-1は1をπラジアンすなわち180度回転したものである。つまり、アフォーダンスを表すベクトルB-Aは「負の型」である環世界を表すベクトルを反転して「正の型」として見たものと見做せる。ちなみに、こういうベクトルを使って対象を表すこと自体が環世界的表現なのである。

興味深いのは「負」が意味を持つということだ。これは松岡さんと私が共通して持っている志向性である。量子論を量子力学に引き上げたハイゼンベルグの行列力学とシュレーディンガーの波動力学とが相互に変換可能、つまり等価であることを示したポール・ディラックが“ディラックの海”として考えた陽電子の仕組みもまた「負」が意味を持つ典型例だ。下図の左に示すように、負のエネルギー領域に電子があるとする。これが何らかのエネルギーをもらって正のエネルギー領域に姿を現したとする（図の右上）。これが我々の宇宙で観測する負の電荷と正のエネルギーを持つ電子（e^–）である。負のエネルギーを持つ電子が抜けた穴（図の右下）は正の電荷をもつ電子、すなわち陽電子（e⁺）である。陽電子は電子の「抜け型」として理解されるというアイデアだった。

2025年度のノーベル化学賞を受賞した北川進氏はナノオーダーの孔を多数持つMOF（金属有機構造体）を開発した。この孔に気体を閉じ込めることができるので、無用である孔（穴）こそが有用であるとして、荘子の「無用の用」（『老子』老子道徳経１１「三十の輻」とも「無の用」ともいわれるものが初出。後に荘子が別の例を使ってその重要性を強調した）が彼の研究を推進した哲学だと言っている。まさに、「負の型」、「抜け型」が意味を持つ好例である。

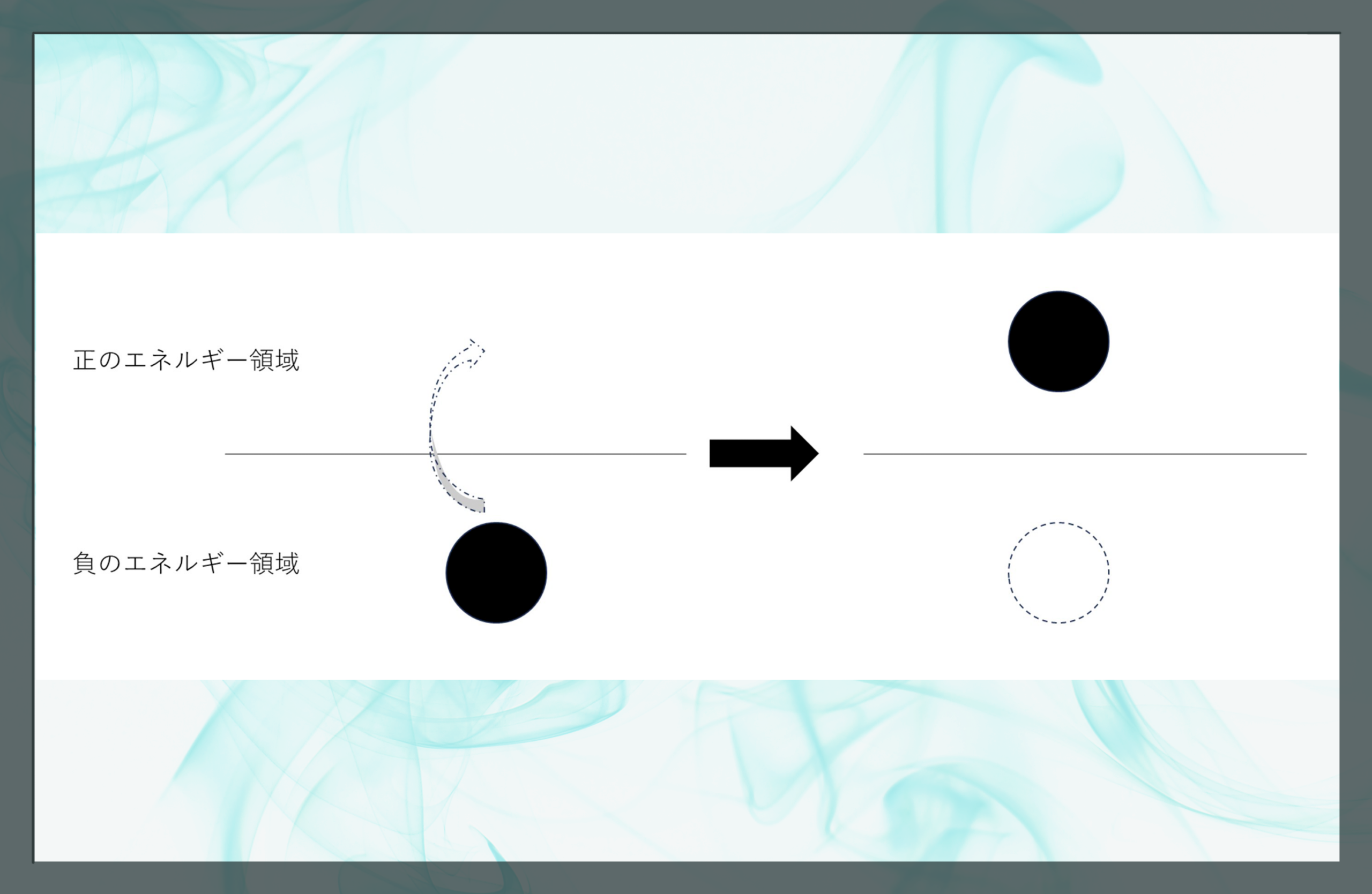
水平線下部が「ディラックの海」。負のエネルギーを持つ電子がぎっしりと埋まっている。ディラックの海にある電子がなんらかのエネルギーをもらって水平線上部に飛び出すと、ぎっしり詰まった場所から一つ電子が抜け、相対的にその「穴」が正の電荷を持っているように振る舞うようになる。「穴」が実在として機能するのである。

斜めは複雑さをもたらす
松岡さんは相当早い時期にロジェ・カイヨワに会いに行っている（第８９９夜、『編集力』pp.58-70）。カイヨワの千夜千冊を見ると、カイヨワ自身がパリが与えた「抜き型」として負の効用を具現化した人だったという想像にかられるのである。カイヨワは類似性を考察することで「方法としての対角線の科学」に踏み出したと松岡さんは書いた。そして、カイヨワがある意味複雑系の科学を志向していたと喝破した。これは面白い。そもそも、対角線のような斜めは織物の世界では複雑性を意味するからだ。縦と横の糸では組めないより複雑な文様は斜めの糸によって創発する。まさに、斜めは複雑性を象徴しているのである。だから、対角線や斜めで考えるのは編集工学や複雑系科学とまさに相容れる方法なのである（田中優子著『不確かな時代の「編集稽古」入門』（朝日新書）p.81）。

カイヨワがダーウィンの自然選択説に文句をつけているところも面白い。ただし、生物進化においては、自然選択が有効な場合、性選択が有効な場合、さらには木村資生のように自然選択とは関わらない中立的な遺伝子が生き残ることが進化に重要な役割を果たすという説もあり、進化に対する駆動力にはさまざまなバージョンが考えられる。それ故にカイヨワの説そのものに賛同することはできないのだが、彼の思想の根底に「でないもの」に注目し、その効用を信じる傾向が見て取れるというところが面白いのだ。これは「ジャック・モノ―じゃない」説を出そうとするところにも表れている。「形成・生成」ではなく、「破壊・崩壊」が生命の熱力学の本質だと考えたところなどだ。「顕れていない」ところに目を向ける天才なのだろう。だから、日本文化と相性も良いのだろうし、松岡さんが目を付けたのもそういったところなのだろう。

さらに、カイヨワは斜めに走る。ユネスコが後援している国際哲学人文科学協議会年報である「ディオゲネス」を1953年に創刊した。私が生まれた年だ。カイヨワはユネスコの職員を務めていたのだからユネスコが後援しているのは自然だが、人文系の総合誌を創刊し、雑誌名を「ディオゲネス」としたところなどは複雑系科学者の精神性の一端が垣間見える。ディオゲネスは古代ギリシャの変わり者の哲学者として知られているが、私にとっては、シャーロック・ホームズの兄マイクロフト・ホームズが創立者の一員になっている「ディオゲネス・クラブ」がこのディオゲネスからとられていることがより面白い。そしてそれが複雑さを表す斜めのカイヨワと結びつくところが面白いのである。

『編集力』にはさらに斜めに走る人が登場する。ジョルジョ・アガンベンだ。松岡さんはスタンツェを千夜千冊した（第１３２４夜、『編集力』pp.108-125）。本来”部屋”を意味するスタンツァに対して、“スタンツァは（単なる物を収容する場所ではなく）ヨーロッパの多くの表象と欲望と言葉とを収容するところで、そこを横切っていくことがスタンツェなのである”と書いている（『編集力』p.118）。特に、アガンベンが「否定の方法」、「負の方法」を確信していたところで共鳴した。まさにこれが複雑さを生みだす方法でもあるからであろう。そして、スラボイ・ジジェックのところで、人間の認知活動には「ないものを代理する作用」、すなわち「負」によって何かが補足される作用があると見抜いたのだった（第６５４夜、『編集力』pp.124-134）。

松岡がカイヨワに相似律特集の割れ目ページ（上図）を見せたとき、彼がとりわけ関心を寄せたのは、乱れた蜘蛛の巣だった。この蜘蛛には、LSDが与えられていたのだ。カイヨワはそこに「破壊・崩壊」の兆しを見ていたのだろうか。

正でも負でもない境界が生み出す複雑さ
『編集力』のもう一つの大きな特徴は、第4章のハイパーテキストだ。そこで、「文巻」の存在が公開された（第１５１９夜、『編集力』pp.338－353）。ここで、松岡さんは編集工学の根幹の方法論を「伏せて、開ける」ことだと書いている。これは松岡さんとの会話でもよく出てくる「いないいない、ばあー」である。これは数学の開集合と閉集合に対して補集合をとる操作に似ている。厳密なことは置くとして、開集合はそこに含まれるどんな点に対してもその近傍内のすべての点がその集合に含まれるような近傍が存在するとして定義される。開集合の補集合は閉集合である。集合Aの補集合は全体集合Xから集合Aを除いた集合X-Aである。しかし、開集合の定義と閉集合の定義は異なった概念に依っていることは注意しないといけない。閉集合は集合内のすべての点の集積点を含むような集合として定義される。集積点というのは点列の極限点の事である。例えば、 B={ $\frac{1}{n}$ ∈Q|n∈N}という集合は、自然数nに対して $\frac{1}{1}$ $\frac{1}{\mathrm{<span\; style="font-family:\; \text{'}book\; antiqua\text{'},\; palatino,\; serif;">,</span>2}}$ $\frac{1}{\mathrm{<span\; style="font-family:\; \text{'}book\; antiqua\text{'},\; palatino,\; serif;">,</span>3}}$  ⋯のような有理数Qの点列からなっている。この極限点（集積点）は自然数n→∞の極限で0である。開集合と閉集合の定義が互いに排他的ではないので、開かつ閉である集合や、開でも閉でもない集合が存在する。また、閉集合は境界を持つが開集合は持たない。実数の集合の部分集合としての有理数の集合は有理点列の極限が無理数になることがある（たとえば、1, 1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414213,…→√2）ので、閉集合ではない。また、どんな有理数の近傍にも無理数が入るから開集合でもない。集合に対して、その内部の点（内点）、外部の点（外点、集合の補集合の内点）と境界点が定義される。境界点はその任意の近傍内に内点も外点も含むような点の集まりである。例えば、実数の位相の下では、有理数の境界は実数全体になり、無理数の境界も実数全体になる。フラクタル図形の境界なども類似の性質を持つ。

「いないいない、ばあー」は集合を見せたり、その補集合を見せたりする操作の中でも、有理数や無理数に対してそれを行っているような印象がある。つまり、例えば、実数という位相に対して、有理数を隠しておいて無理数のみを見せると、境界点としての実数全体が見えてくる。今度は隠していた有理数も見せると見えるのは全体集合としての実数である。そこにはもはや境界という概念はなく全体が見えるのである。「いないいない」で隠れていた時には境界点としてチラチラ見えていたものが、「ばあー」とした途端に全体が見えるという構造になっている。

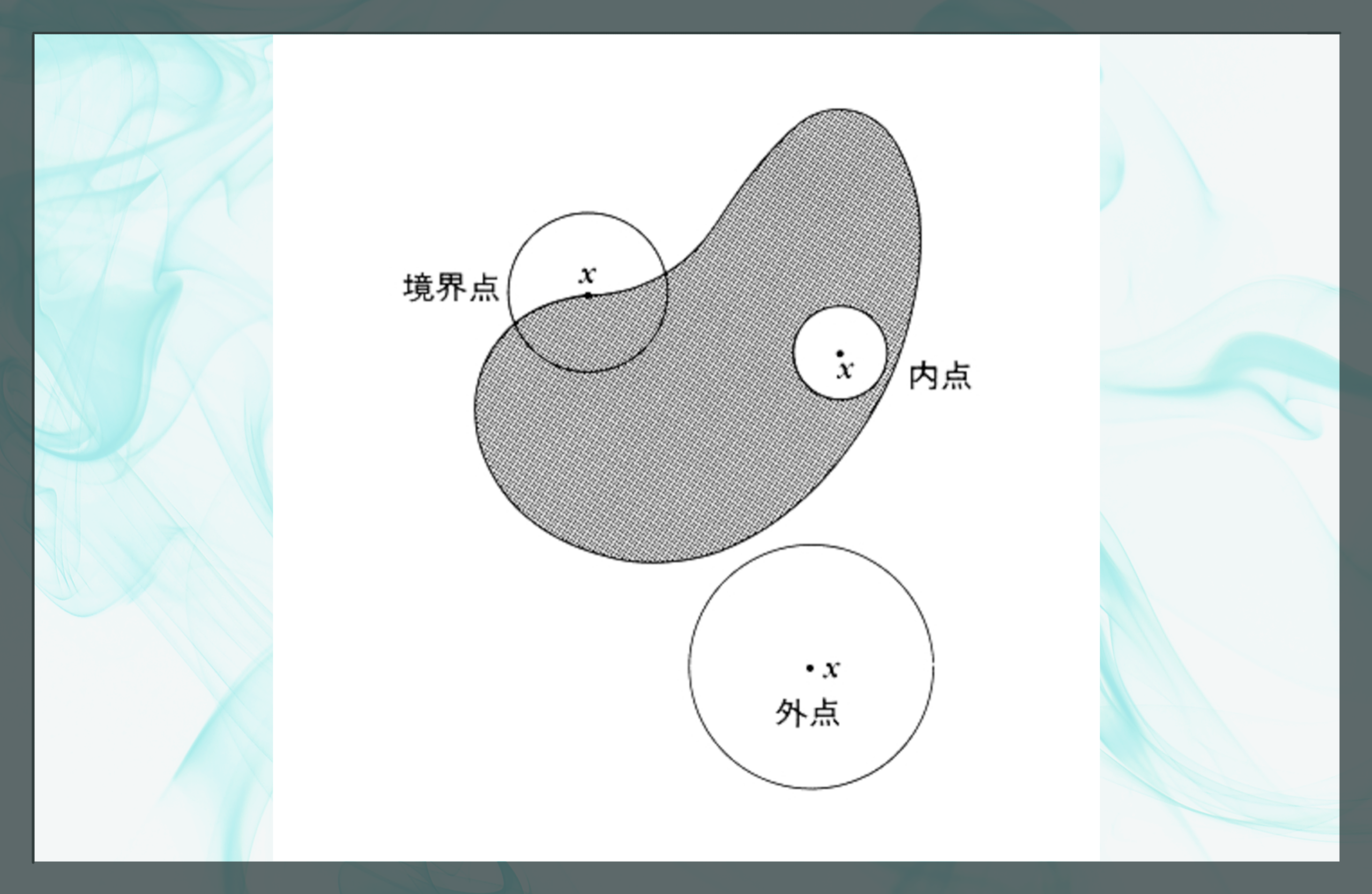
開集合・閉集合の定義の基礎となる点（内点・外点・境界点）の分類を示した模式図。集合がどこまでを含むかは、局所的な近傍の取り方によって定義される。有理数と無理数の集合は実数直線上では互いに稠密に入り組み、任意の実数のどんな近傍にも有理数と無理数が同時に現れる。

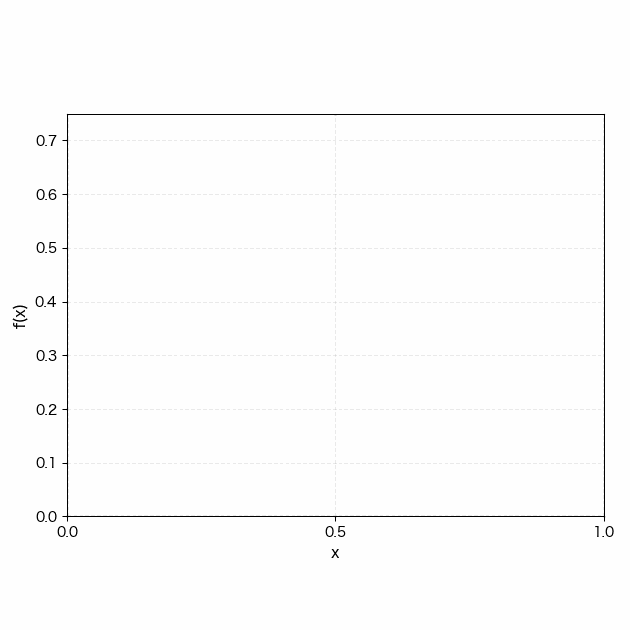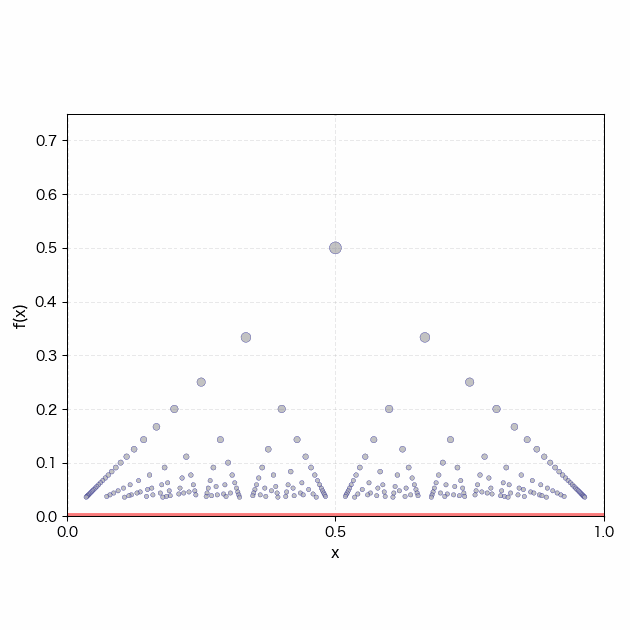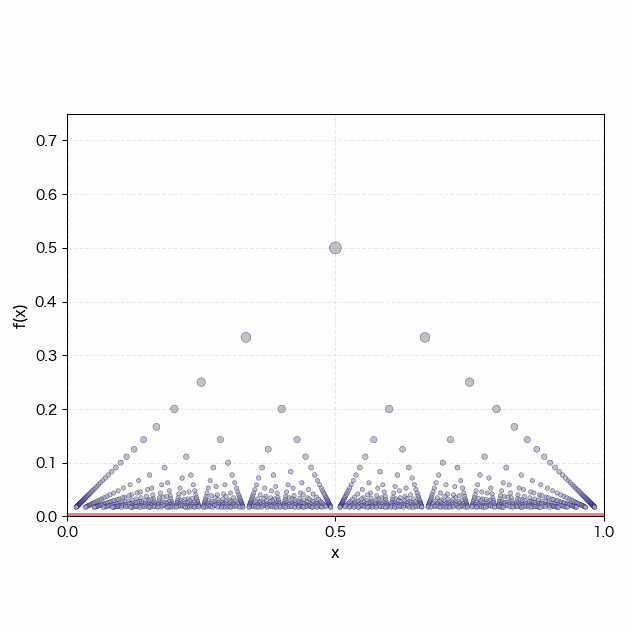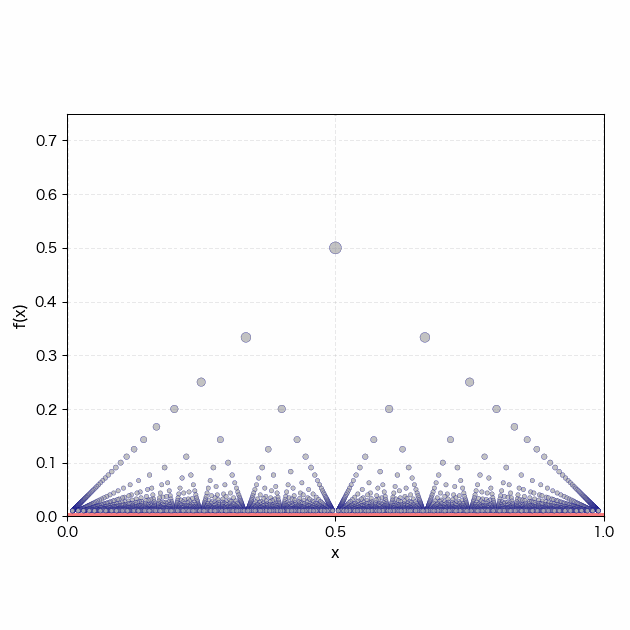
上図はトマエ関数をもとにした集合操作である。xを[0, 1]区間の数としてf(x)を以下で定義する。
f(x)=1/q （x=p/q（既約分数）, p, qは0でない自然数）
=1（x=0）
=0（xが無理数）
横軸は[0, 1]区間である。
まず、無理数集合を表す赤線が実数直線上に現れる。このとき、すべての実数の近傍には無理数と有理数の両方が潜んでいる。つまり、無理数の傍に有理数の気配が「いないいない」している。 赤線の次に登場する青い点群は有理数の集合である。有理数は無理数よりも集合としての濃度が低いため、実数直線上ではほとんど埋没している。しかしトマエ関数に従って[0, 1]区間の有理数点上で定義された関数f(x)を描くと、有理数の気配が実在を伴って「ばあー」し、実数全体の構造が浮かび上がる。

境界をめぐって
松岡さんはマイケル・ポランニーの「暗黙知」の千夜千冊で（第１０４２夜、『編集力』pp.154-162）ソ連指導の共産圏の科学者としてのポランニーに触れている。私の長年の友人であるポランニーと同じハンガリー生まれのピーター・エルディは驚くほど日本人の物理学者、化学者の論文を読んでいた。ハンガリーはマジャール人というアジアに起源を持つ民族がヨーロッパにやってきて作った国を起源に持つ。したがって、ハンガリー人にはその民族的ルーツがアジアにあるという思いが強い人が多い。類似点は姓・名の順で名前を呼び、子供のころには蒙古斑があるなどである。アジア民族への親近感からか、一般にハンガリー人はアジア人には興味を持つようだが、エルディは特に日本人に特別な興味を持っていた。イリア・プリゴジンと共に非平衡物理の研究の先駆者のひとりであるヘルマン・ハーケンが南ドイツのシュロース・エルマウという村のコテージ風会議場で開催したシナジェティクス・シリーズに、1983年清水博先生とともに招待されたときに、シュロース・エルマウへ向かう列車の中でエルディに初めて出会った。すぐに「何者かである」と分かったが、その時はあいさつ程度しかしなかった。その後1984年に、私は「脳の解釈学」に関する論文を京大基礎物理学研究所（湯川研究所）発行の物理の学術誌に出版した。エルディはこれを読んで驚喜したというのだ。それで、彼が勤めるブダペストのハンガリー科学アカデミーに呼んでくれた。夕食を食べるのも忘れてマルギット島を歩きながら質問攻めにあった。多くは学問的な質問だったが、その中で一つ不思議な質問が含まれていた。「東洋と西洋の境界はどこだと思うか？」というのだ。私は、この種の事をあまりまじめに考えたことはなかったのだが、松岡さんがポランニーに見たハンガリー学者の境界に対する強い思いと類似なもののような気がしている。その後、折に触れて彼は私にこの境界の質問を投げかけてきた。我々の間で結論らしきものは出ていないが、研究者はしょせん有理数上にしか存在できない人種（つまり測度ゼロ：測ったら消えてしまう）なのだから、おそらくは境界は世間という実数の位相で見て実数全体なのだろう。そして、「いないいない、ばあー」をすることでその実体は鮮明に見えてくるのではないだろうか。

ポランニーは、言語や数式では分解・理解しきれない情報の流れがこの世界の奥に潜在していて、これが不意に表出するとき科学の大発見が起こると考えた。カイヨワも松岡も、表面的にはなにも関係なさそうな事物の間に「見えない連携」を探すことに熱中していた。上図はカイヨワ『石が書く』より、目玉入りの瑪瑙。カイヨワにはこの石に、円の幾何学も、蛇の皮も、浮世絵の雲海も映り込んでいるように見えていた。自然とは単なるファンタジーではなく、隠された意味を持つアナロジー・システムであると信じていたからだ。カイヨワもポランニーも、そして松岡も、見た目や数式の似ている予感の先に、あらゆる境界がゆらいで起こる「いないいない・ばあ」のもたらす万感を求め遊学していたのだろう。

1.  

2. 図版構成：梅澤光由＆齋藤彬人

3.  

4. ---

5. イシス編集学校56[守]特別講義

6. 津田一郎の編集宣言 -複雑系の守破離 数学と編集工学のインタースコア-

   ●日時：2026年1月25日（日）14:00-17:00
   ●参加方法：オンライン開催　＊お申し込みの方にzoomURLをご案内します
   ●参加費：3,850円（税込）
   ●対象：どなたでも参加いただけます
   ●ゲスト講師：津田一郎さん（ISIS co-mission、数理科学者）

7. ●申込：https://shop.eel.co.jp/products/es_shu_056_toku

8. ＊56期［守］師範・師範代・学衆は教室にてお申し込みください。
   ＊44回［ISIS花伝所］師範・入伝生は連径帖ラウンジにてお申し込みください。
   ＊多読アレゴリア2026冬（2026年1月〜3月）にご参加の皆さまへ
   　当イベントは多読アレゴリア2026冬の無料オンライン視聴特典（1月分）です。多読アレゴリア2026冬の参加者の方は、多読アレゴリアでの案内をご確認ください。

9.  

10. ◇参考動画：
    「編集」を学べば、情報の本質が見えてくる」津田一郎メッセージ
    https://youtu.be/ojQ4yC86WbE

11. ---

12.  

    津田一郎の『千夜千冊エディション』を謎る

    ①『心とトラウマ』に西洋と東洋のAIDAを謎る

    ②『心とトラウマ』に「心の統合」という不思議を謎る

    ③『理科の教室』で偶然の一致あるいは縁を謎る

    ④『理科の教室』で遍歴を謎る

    ⑤『理科の教室』で思索の庭を謎る

13. ⑥『編集力』でアブダクションを謎る
14. ⑦『編集力』で言語の境界を謎る
15. ⑧『編集力』で真似るを謎る
16. ⑨『編集力』で負を謎る